Machine learning for Electric Force Microscopy published in Mater. Charact.
P. Gupta, L. S. Schadler and R. Sundararaman, “Dielectric properties of polymer nanocomposite interphases from electrostatic force microscopy using machine learning”, Mater. Charact. 173, 110909 (2021)
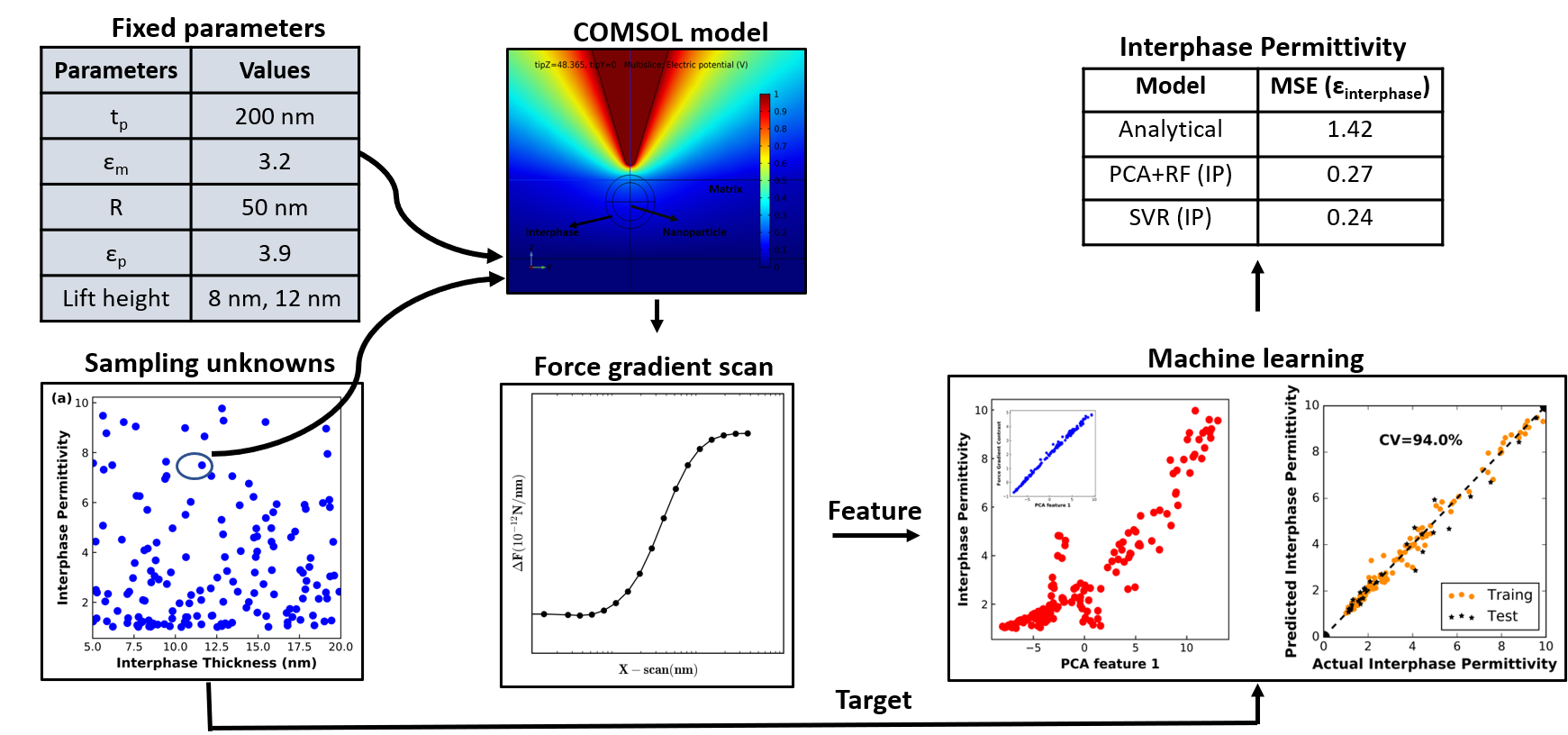
Interphase regions in polymer composite materials strongly influences their mechanical, thermal and dielectric properties but are difficult to characterize due to nanoscale dimensions. Electrostatic force microscopy (EFM) provides a pathway to local dielectric property measurements but extracting dielectric permittivity of interphase from EFM measurements remains a challenge. This is because the measured signal depends on the geometric parameters of the tip and on the dielectric variation within an extended region of the sample in a convolved fashion. This geometric complexity precludes general analytical solutions, and previous studies have relied on several approximations. Moreover, some of these parameters are unknown during experimental setup but affects the raw measurements, further reducing the reliability of analytical predictions. Thus, the key challenge in EFM modeling for extracting interphase dielectric response is the large number of parameters (geometry, dielectric variation) and measurements (2D arrays of force gradients). In this work, we demonstrate the efficacy of machine learning models to extract interphase permittivity using a dataset of synthetic EFM force gradient scans generated by finite element simulations.
We show that both support vector regression and random forest algorithms are able to ‘invert’ the force gradient scan to predict the permittivity with high accuracy using a modest dataset of 200 finite element simulations. Feature reduction by principal component analysis improves the model’s performance and reveals force gradient contrast to be the most important feature in permittivity detection. Our results show that ML models capture significant complexity in the EFM measurements of this system beyond what is possible with previous analytical approaches. In particular, they make it possible to account for unknown experimental parameters such as interphase thickness and particle depth from the force gradient data alone.
